K-means原理、优化及应用
K-Means算法是无监督的聚类算法,它实现起来比较简单,聚类效果也不错,因此应用很广泛。K-Means算法有大量的变体,本文就从最传统的K-Means算法讲起,在其基础上讲述K-Means的优化变体方法。包括初始化优化K-Means++, 距离计算优化elkan K-Means算法和大数据情况下的优化Mini Batch K-Means算法。
K-Means算法的思想很简单,对于给定的样本集,按照样本之间的距离大小,将样本集划分为K个簇。让簇内的点尽量紧密的连在一起,而让簇间的距离尽量的大。
如果用数据表达式表示,假设簇划分为(C1,C2,...Ck)(C1,C2,...Ck),则我们的目标是最小化平方误差E:
E=∑i=1k∑x∈Ci||x?μi||22E=∑i=1k∑x∈Ci||x?μi||22
其中μiμi是簇CiCi的均值向量,有时也称为质心,表达式为:
μi=1|Ci|∑x∈Cixμi=1|Ci|∑x∈Cix
如果我们想直接求上式的最小值并不容易,这是一个NP难的问题,因此只能采用启发式的迭代方法。
K-Means采用的启发式方式很简单,用下面一组图就可以形象的描述。
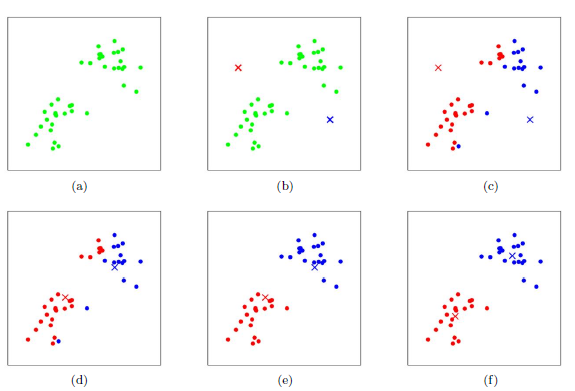
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
? ? ? ? 当然在实际K-Mean算法中,我们一般会多次运行图c和图d,才能达到最终的比较优的类别。
?
算法步骤:
1.(随机)选择K个聚类的初始中心;
2.对任意一个样本点,求其到K个聚类中心的距离,将样本点归类到距离最小的中心的聚类,如此迭代n次;
3.每次迭代过程中,利用均值等方法更新各个聚类的中心点(质心);
4.对K个聚类中心,利用2,3步迭代更新后,如果位置点变化很小(可以设置阈值),则认为达到稳定状态,迭代结束,对不同的聚类块和聚类中心可选择不同的颜色标注。
优点?
1)原理比较简单,实现也是很容易,收敛速度快。?
2)聚类效果较优。?
3)算法的可解释度比较强。?
4)主要需要调参的参数仅仅是簇数k。
缺点?
1)K值的选取不好把握?
2)对于不是凸的数据集比较难收敛?
3)如果各隐含类别的数据不平衡,比如各隐含类别的数据量严重失衡,或者各隐含类别的方差不同,则聚类效果不佳。?
4) 最终结果和初始点的选择有关,容易陷入局部最优。
5) 对噪音和异常点比较的敏感。
? ? ? ?k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。
K-Means++的对于初始化质心的优化策略也很简单,如下:
a)从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1
? ? b) 对于数据集中的每一个点xi,计算它与已选择的聚类中心中最近聚类中心的距离D(xi)=argmin||xi?μr||^2……r=1,2,...kselected
c) 选择下一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大
d) 重复b和c直到选择出k个聚类质心
e) 利用这k个质心来作为初始化质心去运行标准的K-Means算法
K-Means++对初始聚类中心点的选取做了优化,简要来说就是使初始聚类中心点尽可能的分散开来,这样可以有效的减少迭代次数,加快运算速度。
在传统的K-Means算法中,我们在每轮迭代时,要计算所有的样本点到所有的质心的距离,这样会比较的耗时。那么,对于距离的计算有没有能够简化的地方呢?elkan K-Means算法就是从这块入手加以改进。它的目标是减少不必要的距离的计算。那么哪些距离不需要计算呢?
elkan K-Means利用了两边之和大于等于第三边,以及两边之差小于第三边的三角形性质,来减少距离的计算。
第一种规律是对于一个样本点xx和两个质心μj1,μj2。如果我们预先计算出了这两个质心之间的距离D(j1,j2),则如果计算发现2D(x,j1)≤D(j1,j2),我们立即就可以知道D(x,j1)≤D(x,j2)。此时我们不需要再计算D(x,j2),也就是说省了一步距离计算。
? 第二种规律是对于一个样本点x和两个质心μj1,μj2。我们可以得到D(x,j2)≥max{0,D(x,j1)?D(j1,j2)}。这个从三角形的性质也很容易得到。
利用上边的两个规律,elkan K-Means比起传统的K-Means迭代速度有很大的提高。但是如果我们的样本的特征是稀疏的,有缺失值的话,这个方法就不使用了,此时某些距离无法计算,则不能使用该算法。
? ? ? 个人理解,第一个规律简单有效,很容易理解,但是第二个规律对简化运算量的意义不是很大。
在统的K-Means算法中,要计算所有的样本点到所有的质心的距离。如果样本量非常大,比如达到10万以上,特征有100以上,此时用传统的K-Means算法非常的耗时,就算加上elkan K-Means优化也依旧。在大数据时代,这样的场景越来越多。此时Mini Batch K-Means应运而生。
顾名思义,Mini Batch,也就是用样本集中的一部分的样本来做传统的K-Means,这样可以避免样本量太大时的计算难题,算法收敛速度大大加快。当然此时的代价就是我们的聚类的精确度也会有一些降低。一般来说这个降低的幅度在可以接受的范围之内。
在Mini Batch K-Means中,我们会选择一个合适的批样本大小batch size,我们仅仅用batch size个样本来做K-Means聚类。那么这batch size个样本怎么来的?一般是通过无放回的随机采样得到的。
为了增加算法的准确性,我们一般会多跑几次Mini Batch K-Means算法,用得到不同的随机采样集来得到聚类簇,选择其中最优的聚类簇。
该算法的迭代步骤有两步:
1:从数据集中随机抽取一些数据形成小批量,把他们分配给最近的质心
2:更新质心
与K均值算法相比,数据的更新是在每一个小的样本集上。对于每一个小批量,通过计算平均值得到更新质心,并把小批量里的数据分配给该质心,随着迭代次数的增加,这些质心的变化是逐渐减小的,直到质心稳定或者达到指定的迭代次数,停止计算
Mini Batch K-Means比K-Means有更快的?收敛速度,但同时也降低了聚类的效果,但是在实际项目中却表现得不明显。个人理解,Mini Batch K-Means通过小样本的实验,可以初步预测聚类中心的位置,对n次Mini Batch K-Means的聚类结果取均值作为大样本实验初始聚类中心的位置,也能够减少运算量,加快聚类速度。
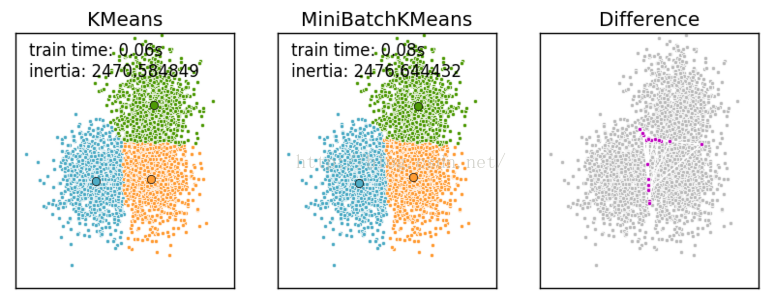
下边给出显示上边这副图的代码,也是对K-Means和Mini Batch K-Means算法的一个比较:
import time
?
import numpy as np
import matplotlib.pyplot as plt
?
from sklearn.cluster import MiniBatchKMeans, KMeans
from sklearn.metrics.pairwise import pairwise_distances_argmin
from sklearn.datasets.samples_generator import make_blobs
?
##############################################################################
# Generate sample data
np.random.seed(0)
?
batch_size = 45
centers = [[1, 1], [-1, -1], [1, -1]] #初始化三个中心
n_clusters = len(centers) ? ? ? #聚类的数目为3
#产生3000组两维的数据,以上边三个点为中心,以(-10,10)为边界,数据集的标准差是0.7
X, labels_true = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7)
?
##############################################################################
# Compute clustering with Means
?
k_means = KMeans(init='k-means++', n_clusters=3, n_init=10)
t0 = time.time() #当前时间
k_means.fit(X)
#使用K-Means 对 3000数据集训练算法的时间消耗
t_batch = time.time() - t0
?
##############################################################################
# Compute clustering with MiniBatchKMeans
?
mbk = MiniBatchKMeans(init='k-means++', n_clusters=3, batch_size=batch_size,
? ? ? ? ? ? ? ? ? ? ? n_init=10, max_no_improvement=10, verbose=0)
t0 = time.time()
mbk.fit(X)
#使用MiniBatchKMeans 对 3000数据集训练算法的时间消耗
t_mini_batch = time.time() - t0
?
##############################################################################
# Plot result
?
#创建一个绘图对象, 并设置对象的宽度和高度, 如果不创建直接调用plot, Matplotlib会直接创建一个绘图对象
'''
当绘图对象中有多个轴的时候,可以通过工具栏中的Configure Subplots按钮,
交互式地调节轴之间的间距和轴与边框之间的距离。
如果希望在程序中调节的话,可以调用subplots_adjust函数,
它有left, right, bottom, top, wspace, hspace等几个关键字参数,
这些参数的值都是0到1之间的小数,它们是以绘图区域的宽高为1进行正规化之后的坐标或者长度。
'''
fig = plt.figure(figsize=(8, 3))
fig.subplots_adjust(left=0.02, right=0.98, bottom=0.05, top=0.9)
colors = ['#4EACC5', '#FF9C34', '#4E9A06']
?
# We want to have the same colors for the same cluster from the
# MiniBatchKMeans and the KMeans algorithm. Let's pair the cluster centers per
# closest one.
k_means_cluster_centers = np.sort(k_means.cluster_centers_, axis=0)
mbk_means_cluster_centers = np.sort(mbk.cluster_centers_, axis=0)
k_means_labels = pairwise_distances_argmin(X, k_means_cluster_centers)
mbk_means_labels = pairwise_distances_argmin(X, mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? mbk_means_cluster_centers)
?
# KMeans
ax = fig.add_subplot(1, 3, 1) #add_subplot ?图像分给为 一行三列,第一块
for k, col in zip(range(n_clusters), colors):
? ? my_members = k_means_labels == k
? ? cluster_center = k_means_cluster_centers[k]
? ? ax.plot(X[my_members, 0], X[my_members, 1], 'w',
? ? ? ? ? ? markerfacecolor=col, marker='.')
? ? ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
? ? ? ? ? ? markeredgecolor='k', markersize=6)
ax.set_title('KMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, ?'train time: %.2fs
inertia: %f' % (
? ? t_batch, k_means.inertia_))
?
# MiniBatchKMeans
ax = fig.add_subplot(1, 3, 2)#add_subplot ?图像分给为 一行三列,第二块
for k, col in zip(range(n_clusters), colors):
? ? my_members = mbk_means_labels == order[k]
? ? cluster_center = mbk_means_cluster_centers[order[k]]
? ? ax.plot(X[my_members, 0], X[my_members, 1], 'w',
? ? ? ? ? ? markerfacecolor=col, marker='.')
? ? ax.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
? ? ? ? ? ? markeredgecolor='k', markersize=6)
ax.set_title('MiniBatchKMeans')
ax.set_xticks(())
ax.set_yticks(())
plt.text(-3.5, 1.8, 'train time: %.2fs
inertia: %f' %
? ? ? ? ?(t_mini_batch, mbk.inertia_))
?
# Initialise the different array to all False
different = (mbk_means_labels == 4)
ax = fig.add_subplot(1, 3, 3)#add_subplot ?图像分给为 一行三列,第三块
?
for k in range(n_clusters):
? ? different += ((k_means_labels == k) != (mbk_means_labels == order[k]))
?
identic = np.logical_not(different)
ax.plot(X[identic, 0], X[identic, 1], 'w',
? ? ? ? markerfacecolor='#bbbbbb', marker='.')
ax.plot(X[different, 0], X[different, 1], 'w',
? ? ? ? markerfacecolor='m', marker='.')
ax.set_title('Difference')
ax.set_xticks(())
ax.set_yticks(())
?
plt.show()
运行结果如下:
?
初学者很容易把K-Means和KNN搞混,两者其实差别还是很大的。
K-Means是无监督学习的聚类算法,没有样本输出;而KNN是监督学习的分类算法,有对应的类别输出。KNN基本不需要训练,对测试集里面的点,只需要找到在训练集中最近的k个点,用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程,找到k个类别的最佳质心,从而决定样本的簇类别。
当然,两者也有一些相似点,两个算法都包含一个过程,即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。
列个表格对比一下特点:
| KNN | K-Means |
| 1.KNN是分类算法? ? 2.监督学习? 3.喂给它的数据集是带label的数据,已经是完全正确的数据 | 1.K-Means是聚类算法? ? 2.非监督学习? 3.喂给它的数据集是无label的数据,是杂乱无章的,经过聚类后才变得有点顺序,先无序,后有序 |
| 没有明显的前期训练过程,属于memory-based learning | 有明显的前期训练过程 |
| K的含义:来了一个样本x,要给它分类,即求出它的y,就从数据集中,在x附近找离它最近的K个数据点,这K个数据点,类别c占的个数最多,就把x的label设为c | K的含义:K是人工固定好的数字,假设数据集合可以分为K个簇,由于是依靠人工定好,需要一点先验知识 |
| ? | ? |
| 相似点:都包含这样的过程,给定一个点,在数据集中找离它最近的点。即二者都用到了NN(Nears Neighbor)算法,一般用KD树来实现NN。 | |
?
7.应用实例
执行夏宫(中国)图像的逐像素矢量量化(VQ),将显示图像所需的颜色数量从96,615种独特颜色减少到64,同时保持整体外观质量。
在该示例中,像素在3D空间中表示,并且K均值用于找到64个颜色簇。在图像处理文献中,从K-means(聚类中心)获得的码本被称为调色板。使用单个字节,可以寻址多达256种颜色,而RGB编码每个像素需要3个字节。例如,GIF文件格式使用这样的调色板。
为了比较,还示出了使用随机码本(随机拾取的颜色)的量化图像。
?
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import pairwise_distances_argmin
from sklearn.datasets import load_sample_image
from sklearn.utils import shuffle
from time import time
n_colors = 64
# Load the Summer Palace photo
china = load_sample_image("china.jpg")
# Convert to floats instead of the default 8 bits integer coding. Dividing by
# 255 is important so that plt.imshow behaves works well on float data (need to
# be in the range [0-1])
china = np.array(china, dtype=np.float64) / 255
# Load Image and transform to a 2D numpy array.
w, h, d = original_shape = tuple(china.shape)
assert d == 3
image_array = np.reshape(china, (w * h, d))
print("Fitting model on a small sub-sample of the data")
t0 = time()
image_array_sample = shuffle(image_array, random_state=0)[:1000]
kmeans = KMeans(n_clusters=n_colors, random_state=0).fit(image_array_sample)
print("done in %0.3fs." % (time() - t0))
# Get labels for all points
print("Predicting color indices on the full image (k-means)")
t0 = time()
labels = kmeans.predict(image_array)
print("done in %0.3fs." % (time() - t0))
codebook_random = shuffle(image_array, random_state=0)[:n_colors + 1]
print("Predicting color indices on the full image (random)")
t0 = time()
labels_random = pairwise_distances_argmin(codebook_random,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? image_array,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? axis=0)
print("done in %0.3fs." % (time() - t0))
def recreate_image(codebook, labels, w, h):
? ? """Recreate the (compressed) image from the code book & labels"""
? ? d = codebook.shape[1]
? ? image = np.zeros((w, h, d))
? ? label_idx = 0
? ? for i in range(w):
? ? ? ? for j in range(h):
? ? ? ? ? ? image[i][j] = codebook[labels[label_idx]]
? ? ? ? ? ? label_idx += 1
? ? return image
# Display all results, alongside original image
plt.figure(1)
plt.clf()
ax = plt.axes([0, 0, 1, 1])
plt.axis('off')
plt.title('Original image (96,615 colors)')
plt.imshow(china)
plt.figure(2)
plt.clf()
ax = plt.axes([0, 0, 1, 1])
plt.axis('off')
plt.title('Quantized image (64 colors, K-Means)')
plt.imshow(recreate_image(kmeans.cluster_centers_, labels, w, h))
plt.figure(3)
plt.clf()
ax = plt.axes([0, 0, 1, 1])
plt.axis('off')
plt.title('Quantized image (64 colors, Random)')
plt.imshow(recreate_image(codebook_random, labels_random, w, h))
plt.show()
第二个例子:
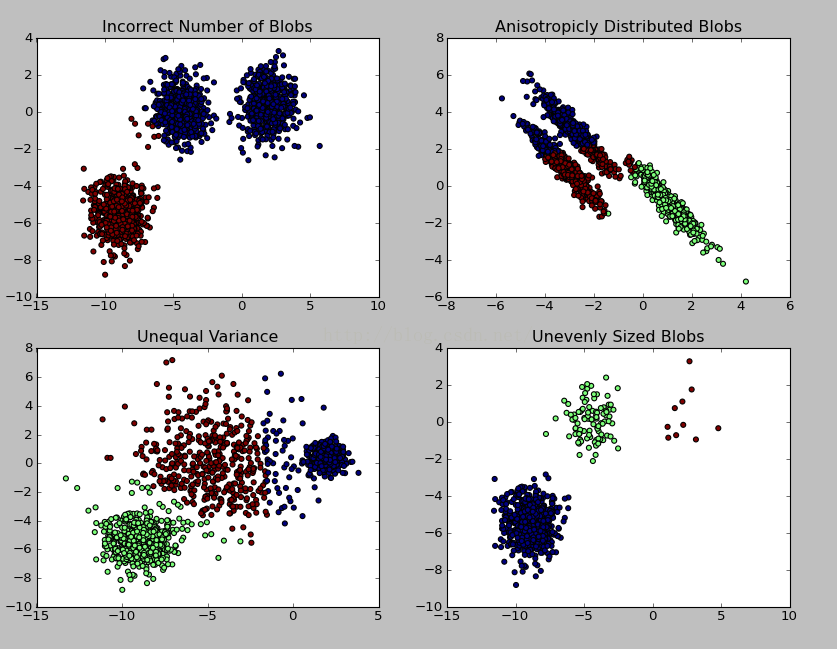
实例说明:利用sklearn.datasets.make_blobs产生1500条两维的数据集进行不同情况下的聚类示例,参见网址:https://blog.csdn.net/gamer_gyt/article/details/51244850
代码如下
import numpy as np ? ? ?#科学计算包
import matplotlib.pyplot as plt ? ? ?#python画图包
?
from sklearn.cluster import KMeans ? ? ? #导入K-means算法包
from sklearn.datasets import make_blobs
?
plt.figure(figsize=(12, 12))
?
"""
make_blobs函数是为聚类产生数据集
产生一个数据集和相应的标签
n_samples:表示数据样本点个数,默认值100
n_features:表示数据的维度,默认值是2
centers:产生数据的中心点,默认值3
cluster_std:数据集的标准差,浮点数或者浮点数序列,默认值1.0
center_box:中心确定之后的数据边界,默认值(-10.0, 10.0)
shuffle :洗乱,默认值是True
random_state:官网解释是随机生成器的种子
更多参数即使请参考:http://scikit-learn.org/dev/modules/generated/sklearn.datasets.make_blobs.html#sklearn.datasets.make_blobs
"""
n_samples = 1500
random_state = 170
X, y = make_blobs(n_samples=n_samples, random_state=random_state)
?
?
# Incorrect number of clusters
y_pred = KMeans(n_clusters=2, random_state=random_state).fit_predict(X)
?
plt.subplot(221) ?#在2图里添加子图1
plt.scatter(X[:, 0], X[:, 1], c=y_pred) #scatter绘制散点
plt.title("Incorrect Number of Blobs") ? #加标题
?
# Anisotropicly distributed data
transformation = [[ 0.60834549, -0.63667341], [-0.40887718, 0.85253229]]
X_aniso = np.dot(X, transformation) ? ?#返回的是乘积的形式
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_aniso)
?
plt.subplot(222)#在2图里添加子图2
plt.scatter(X_aniso[:, 0], X_aniso[:, 1], c=y_pred)
plt.title("Anisotropicly Distributed Blobs")
?
# Different variance
X_varied, y_varied = make_blobs(n_samples=n_samples,
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? cluster_std=[1.0, 2.5, 0.5],
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? random_state=random_state)
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_varied)
?
plt.subplot(223)#在2图里添加子图3
plt.scatter(X_varied[:, 0], X_varied[:, 1], c=y_pred)
plt.title("Unequal Variance")
?
# Unevenly sized blobs
X_filtered = np.vstack((X[y == 0][:500], X[y == 1][:100], X[y == 2][:10]))
y_pred = KMeans(n_clusters=3, random_state=random_state).fit_predict(X_filtered)
?
plt.subplot(224)#在2图里添加子图4
plt.scatter(X_filtered[:, 0], X_filtered[:, 1], c=y_pred)
plt.title("Unevenly Sized Blobs")
?
plt.show() #显示图</span>
?
参考网址:
https://www.cnblogs.com/pinard/p/6164214.html
https://blog.csdn.net/sinat_35512245/article/details/55051306
https://en.wikipedia.org/wiki/K-means_clustering
?